みなさん、こんにちは、
みむすたーです。
今日は前回の「今さらですが、統計学の復習のお時間です」の第1回に引き続き、
第二回の正規分布の説明をしていきたいと思います。
それでは、いきましょう。
もくじ
正規分布とは
生物学や心理学、経済学などの
確率的にできたもの、確率的に起こった事象、
はこの正規分布に従ってデータにばらつきが出ることが知られています。
ただし、正規分布はあくまでばらついたデータの理想モデルであるため、
必ずしも確率的なものや事象が正規分布の通りとなるとは限りません。
正規分布に従う例としては、学校の試験の点数や身長の高さなどが挙げられます。
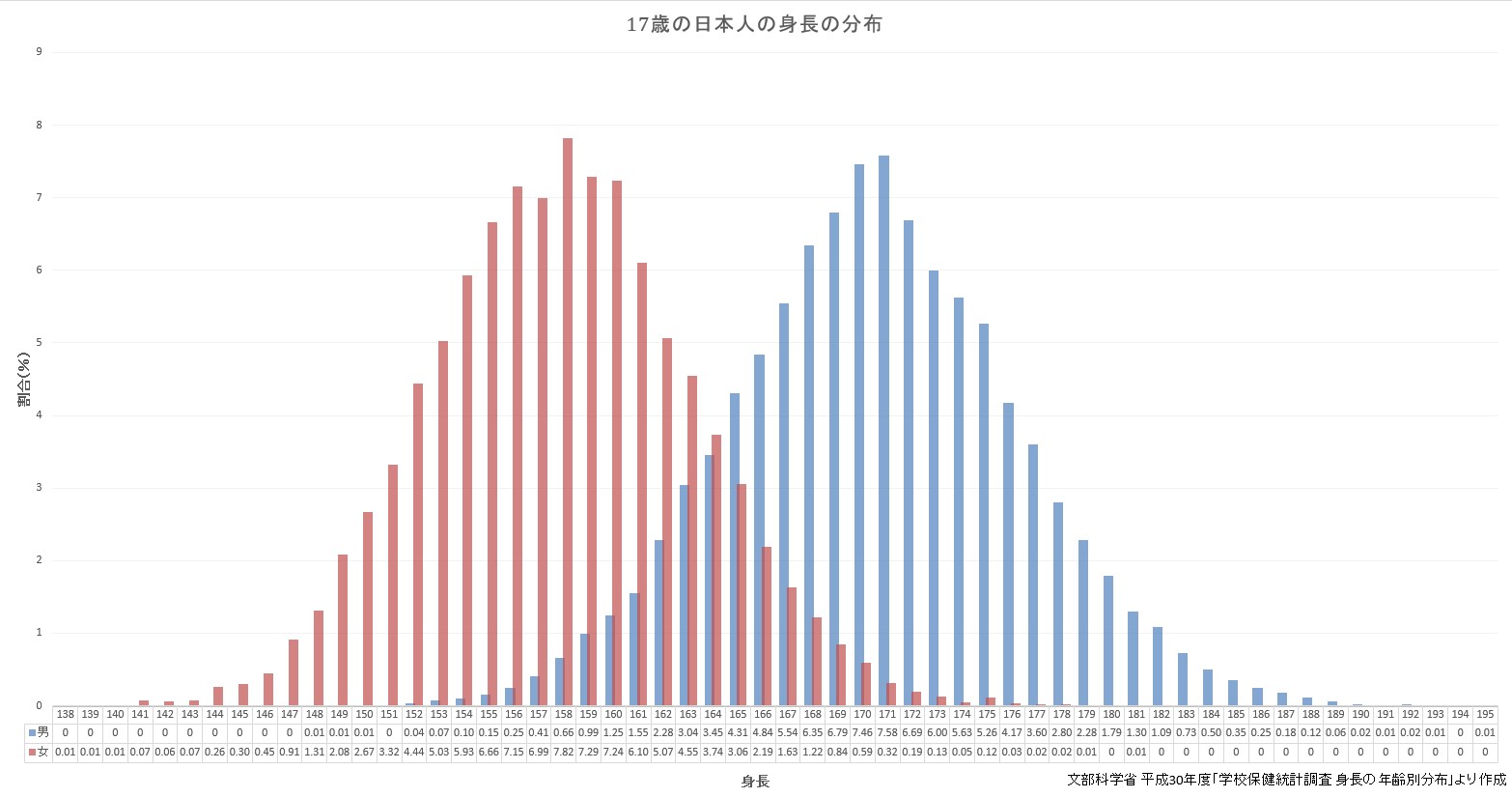
以下の画像は、文部科学相が出している17歳の日本人の身長の分布です。
青い帯が男性の人数、赤い帯が女性の人数を表しています。
帯が高くなるほど帯の下に書いてある身長の人数が多いことになります。
これを一般的にヒストグラムと呼びます。
正規分布が成り立つ理由
ではなぜ、学校の試験の点数や身長の高さが正規分布に従うのかというと、
様々な確率の組み合わせからそのようになると考えられています。
例えば、学校の試験の点数
親から子供が良い教育を受ける確率
学校の授業について行けるかどうかの確率
学校の教師が教え上手である確率
例えば、身長の高さであれば、
今まで身体に良いものを食べてきたかどうかの確率
遺伝的に身長が高い家系である確率
当然ですが、一概に上の事象によって、
結果がそうなるとは限らないのです。
親から子供が良い教育を受けたところで、
その子供が学校の試験の点数にそれを結びつけられるか、
これもまた確率になります。
あくまで確率の話で、これらの確率の組み合わせによって、
データが確率的に正規分布に従うと考えられています。
正規分布の確率密度関数
\[f(x)=\frac{1}{\sqrt{2πσ}}e^{-\frac{(x-μ)^2}{2σ^2}}\]
正規分布は上記のような式で表されます。
確率密度関数とは、あるデータがどの程度の確率で存在するかを表すものです。
例えば、先ほどの身長のグラフで言うと、
身長176cmの人がどの程度の確率で存在するかを表します。
一旦、今日はこの辺りで終わります。
上記の式の導出方法については、また次の回に紹介します。


コメント