みなさん、こんにちは、
みむすたーです。
今日は、人工知能分野の勉強をする上で、必ずと言っても良いほどよく見かける、
勾配降下法について述べていきたいと思います。
勾配降下法とは
まずはそもそも、勾配降下法とは何なのでしょうか。
勾配降下法は、なめらかな関数においてその関数がとりうる最小値を求める手段です。
例えば、以下のような関数の最小値を求めることを考えてみましょう。
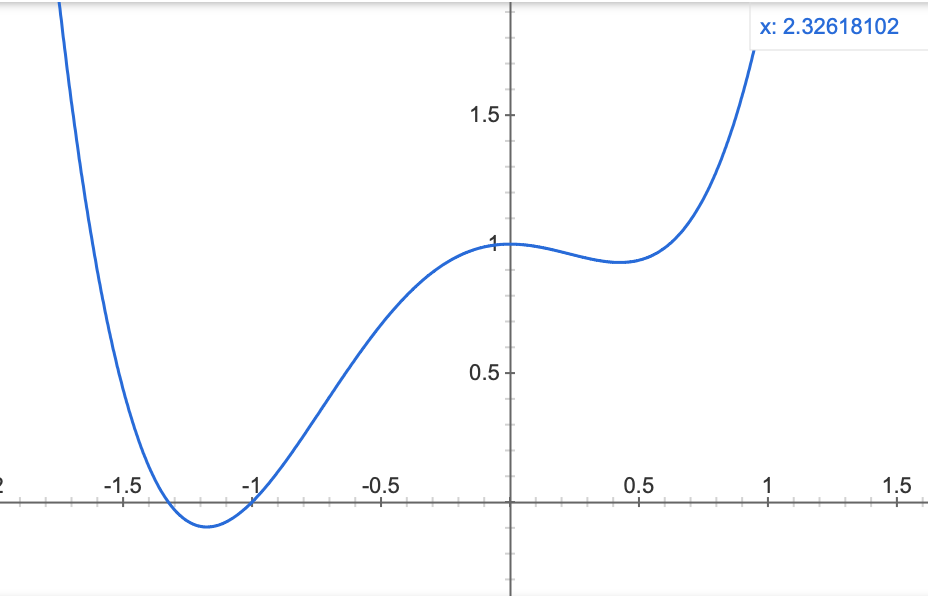
最小値を求める前に、以下のように、まずは、適当な場所に点を打ちましょう。
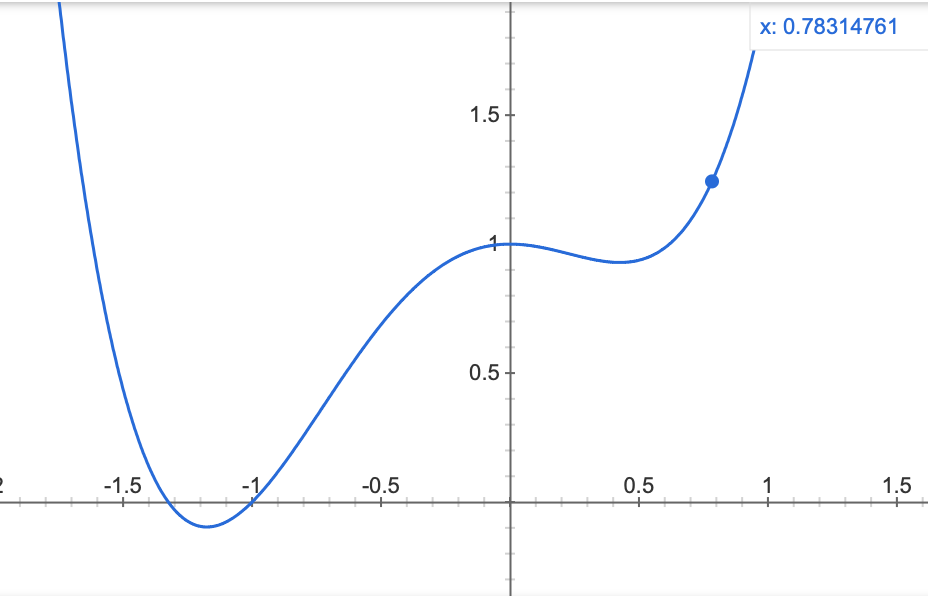
勾配降下法では、この点の位置を移動し、この関数の取りうる最小値を探し出します。
ここで、山に登った後、山から下山する自分が点の位置にいるとイメージするとわかりやすいです。
最小値を取りうる場所に行くために、どのように行動するべきでしょうか。
選択肢としては、左(x軸の負の方向)に向かうか右(x軸の正の方向)に向かうかの2択です。
もちろん、上のグラフを見れば明らかで、左に行くことで最小値に近づきます。
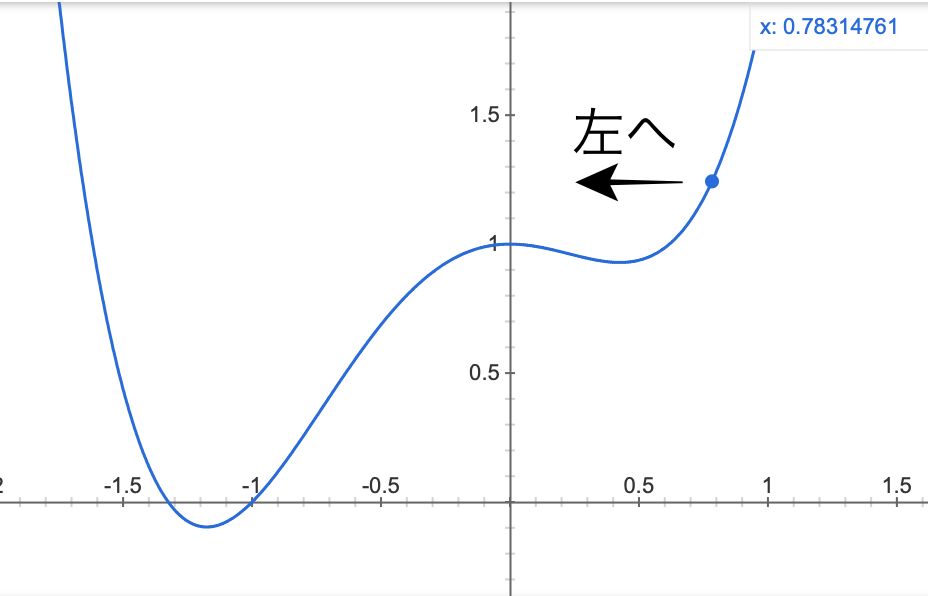
上のような2次元のグラフであれば、どちらに向かうべきかはグラフ化すれば明らかなのですが、
4次元、5次元、・・・と高次元なるにつれ、その想像が不可能になります。
そのため、どちらに向かうべきかを知るために、微分を行います。
4次元、5次元になろうと、なめらかな関数であれば、
微分を行うことでどちらに傾いているのかを把握できます。
微分を行った上で、下に向かう方に少しずつ移動し、最小値を探すというのが勾配降下法です。


コメント